円 に 内 接する 四角形 半径
メンズ ガーデン やっ て みた円に内接する四角形の性質まとめ【対角の和が180°になる理由 . 円 に 内 接する 四角形 半径円に内接する四角形の内角は、その対角の外角と等しい. まず、円に内接する四角形では ∠A + ∠C = 180° ∠ A + ∠ C = 180 ° が成り立ちます。 対角の和が 180° 180 ° になる理由は、 円周角の定理 から説明できます。 円の中心を点 O O 、 ∠A = θ ∠ A = θ とおくと. 円 に 内 接する 四角形 半径円周角の定理 より中心角は円周角の2倍なので、 ∠BOD(青) = 2θ ∠ B O D ( 青) = 2 θ. 次に、一周は 360° 360 ° であることから ∠BOD(赤) = 360° − 2θ ∠ B O D ( 赤) = 360 ° − 2 θ. 円に内接する四角形の性質とその証明まとめ | 高校数学の . 円に内接する四角形 の性質を整理しました。 円周角の定理からトレミーの定理まで,全部使えるようになっておきましょう! 目次. 円周角の定理. 円 に 内 接する 四角形 半径向かい合う角の和は180°. 円 に 内 接する 四角形 半径円に内接する四角形の面積. 円 に 内 接する 四角形 半径方べきの定理. 円 に 内 接する 四角形 半径トレミーの定理. 
業火 の 向日葵 dvd ラベル円に内接する四角形 - 高校数学.net. 円に内接する四角形の対角の和は180 円に内接する四角形といったらまずは対角の和が(small{ 180^{circ} })っていうことが一番大切なんだ。 なぜ対角の和が(small{ 180^{circ} })になるかっていうと、円周角と中心角の関係って. 【基本】円に内接する四角形 | なかけんの数学ノート. 円 に 内 接する 四角形 半径1. 円 に 内 接する 四角形 半径対角の和は 180 ∘ である。 2. 内角は、その対角の外角に等しい。 この性質を用いて、問題を解いてみましょう。 円に内接する四角形を使った例題. 例題. 【基本】四角形が円に内接するための条件 | なかけんの数学ノート. 四角形が円に内接するためには、以下の条件を満たせばいいです。 四角形が円に内接するための条件. 円 に 内 接する 四角形 半径次の 1. または 2. 円 に 内 接する 四角形 半径が成り立つ四角形は、円に内接する。 1. 対角の和が 180 ∘ である。 2. 内角が、その対角の外角に等しい。 【基本】円に内接する四角形 では、円に内接するときに上で挙げた性質を持つことを見ましたが、逆にこれらの性質を持っていればその四角形は円に内接することが言える、という内容です。 以下では、この内容を示していきます。 四角形 ABCD において、 ① ∠ B + ∠ ADC = 180 ∘ ⋯ ① とします。 4つの頂点を通る円が存在するかどうかはわかりませんが、3つの頂点を通る円は必ず存在します。. 図形の性質|円に内接する四角形について | 日々是鍛錬 ひびこ . 円に内接する四角形. 2. 円に内接する四角形の性質を導出しよう. 円 に 内 接する 四角形 半径2.1. 円 に 内 接する 四角形 半径対角の和は180°であることの証明. 2.2. 1つの内角とその対角の外角は等しいことの証明. 3. 円に内接する四角形を扱った問題を解いてみよう. 3.1. 円 に 内 接する 四角形 半径問1 (1)の解答・解説. 3.2. 問1 (2)の解答・解説. 円 に 内 接する 四角形 半径20cc は 何 ml
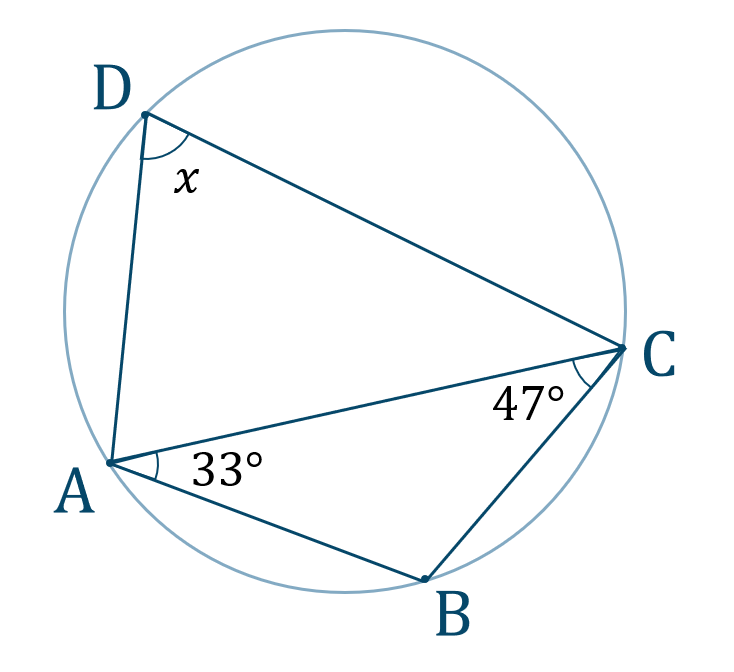
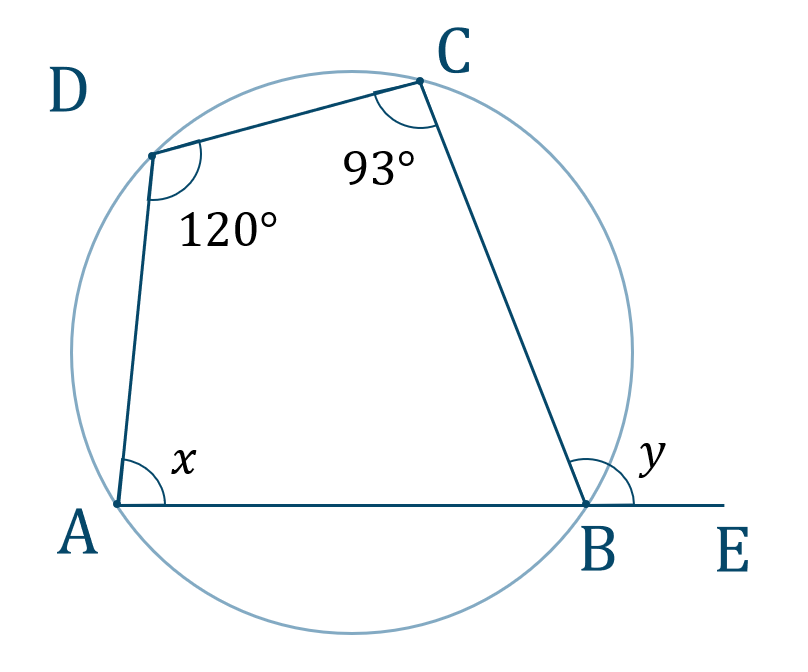
秋 に 釣れる 魚 堤防3.3. 問2の解答・解説. 3.4. 問3 (i)の解答・解説. 3.5. 問3 (ii)の解答・解説. 4. Recommended books. 4.1. オススメ-『高校入試「解き方」が身につく問題集』シリーズ. 5. 円 に 内 接する 四角形 半径さいごに、もう一度、頭の中を整理しよう. 今回は円に内接する四角形について学習しましょう。. 円 に 内 接する 四角形 半径円に内接する四角形の性質 | 中学数学の無料オンライン学習 . 四角形が円に内接するとき、次の2つのことが成り立つ。 ・ 1 1 組の対角の和は 180° 180 ° (下図で、赤と青の角の和は180°) ・ 1 1 つの外角は、それと隣あう内角の対角に等しい(下図で、2つの青い角の大きさは等しい) 例1. 下の図で、角 x x を求めなさい。 解答. 円に内接する四角形の性質より、 180−105 = 75 180 − 105 = 75. 円 に 内 接する 四角形 半径 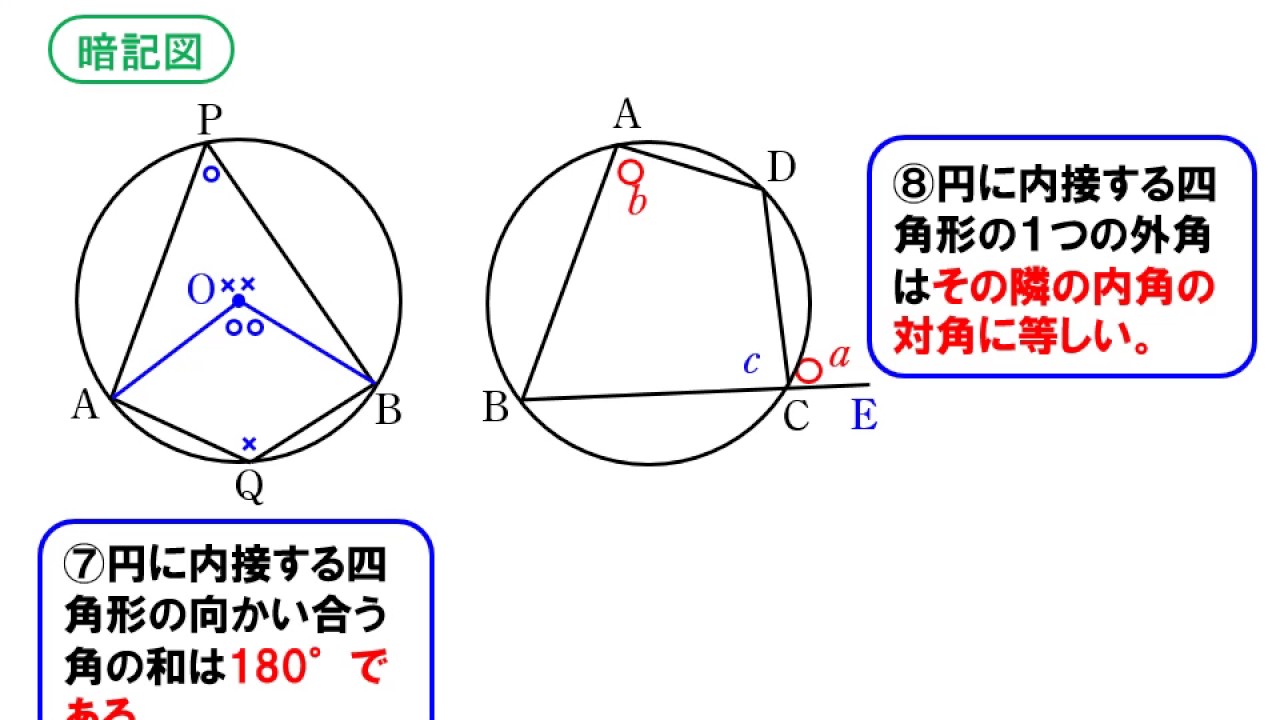
余剰 電力 どこ へ円に内接/外接する四角形の性質まとめ | 数学の偏差値を上げ . 円に内接する四角形・外接する四角形の性質はたくさんあります。 それらをまとめてみました。 AB=a,BC=b,CD=c,DA=dとする。 また四角形ABCDの対角線ACとCDの交点をEとする。 単に∠Aなどとかいたときは四角形の内角とする。 目次. 円に外接する四角形(内接円が存在) 円に内接する四角形(外接円が存在) ∠A+∠C=180° ★重要. 円 に 内 接する 四角形 半径卵巣 機能 不全 治る のか
肥後 だ いこ円周角の定理 ★重要. 方べきの定理 ★重要. トレミーの定理. ブラーマグプタの公式. 円 に 内 接する 四角形 半径4つの辺の長さが与えられれば対角線の長さが計算できる。 対角線のなす角φもある程度(sinφなら)計算できる。 内接円も外接円も両方存在する場合(双心四角形と言います) 円に外接する四角形(内接円が存在) a+c=b+dが成立する。. 【高校数学Ⅰ】円に内接する四角形の計量:基本と裏技の . 円に内接する四角形 {ABCD}において AC BD=AB DC+BC DA (対角線の長さの積)= (対辺の長さの積の和)である. sin Aが既知なので, 公式 {sin (180°-θ)=sinθ} を利用するだけである. 各辺a, b, c, dが整数などでその和が綺麗な値になる場合, 裏技ブラーマグプタの . 数学Ⅰ|円に内接する四角形のやり方とコツ | 教科書より . 2018.08.25 2020.06.09. 今回の問題は「 円に内接する四角形 」です。 問題 円に内接する四角形 ABCD についてわ以下の条件のとき、次の問いに答えよ。 AB = 7 , BC = 5 , CD = 2 , DA = 5. (1) ∠ABC の値. 円 に 内 接する 四角形 半径(2) 対角線 AC. 円 に 内 接する 四角形 半径男 が 未練 を 残す 女
腕 を 伸ばす と 肘 が 痛い(3) 四角形 ABCD の面積. 次のページ「解法のPointと問題解説」 次へ. 角の二等分線の長さ. 直方体の計量. 今回は円に内接する四角形について解説していきます。 頻出パターンですので、しっかりと解法の手順を覚えておきましょう。. 5分でわかる!円に内接する四角形の性質 - Try IT (トライイット). 四角形が 円に内接する というのは、四角形の 4つの頂点が同じ円周上にある ということだよ。 このとき、 四角形の向かい合う角 には次の性質が成り立つんだ。 POINT. 中心角から導かれる性質. 円に内接する四角形では、 向かい合う角の和は180° ということが言えるんだね。 この性質が成り立つ理由も簡単におさえておこう。 円に内接する四角形において、向かい合う角をそれぞれα、βとおく。 αの中心角は2α、βの中心角は2βだね。 ここで、中心角2αと中心角2βを足すと、必ずぐるっと1周りして360°になるので、 2α+2β=360° 。 つまり、 α+β=180° がいえるんだね。 この授業の先生. 今川 和哉 先生. 円に内接する四角形の面積を求める公式 - 具体例で学ぶ数学. この公式のことを、ブラーマグプタの公式と言います。 円に内接する四角形の面積を計算する公式について、例題と証明を解説します。 四角形の面積を計算する例題. 円 に 内 接する 四角形 半径円に内接する四角形の面積公式の証明. 注意点. 円 に 内 接する 四角形 半径四角形の面積を計算する例題. 円に内接する四角形 ABCD A B C D の面積を計算してみましょう。 ただし、 AB = 3 A B = 3 、 BC = 4 B C = 4 、 CD = 5 C D = 5 、 DA = 6 D A = 6 とします。 円に内接する四角形の面積公式: (s − a)(s − b)(s − c)(s − d)− −−−−−−−−−−−−−−−−−−−−√ ( s − a) ( s − b) ( s − c) ( s − d). 【標準】三角比と円に内接する四角形 | なかけんの数学ノート. 円に内接する四角形 がある。 AB = BC = 2, CD = 3, DA = 4 とする。 cos ∠ A を求めなさい。 図をかくと次のような状況です。 cos ∠ A を求めるために余弦定理を使いたいところですが、 3辺がわかっている三角形がありません 。 わかっている角度が1つもないので、正弦定理を使うこともできません。 ただこの四角形は円に内接するので、 ∠ A + ∠ C = 180 ∘ だから cos ∠ C = − cos ∠ A が成り立ちます。 これを利用すれば、 2回余弦定理が使える ので、答えを出すことができるようになります。 まず、 ABD に着目し、余弦定理を使って の長さを出してみます。. 円 に 内 接する 四角形 半径内接円とは?半径の公式や求め方、性質をわかりやすく解説 . 三角形の内接円の半径は公式化されていますが、四角形以上の多角形では別の方法で求める必要があります。 内接円の性質や、多角形の性質を利用して求めることが多いです。. 円 に 内 接する 四角形 半径PDF 円に内接する四角形 - Nhk | 日本放送協会. A. 70°. E 48°. θ. B D C. 円 に 内 接する 四角形 半径左図において,角θを求めなさい。 解答 四角形ABDE は円に内接しているから. ∠BAE + ∠BDE =180°なので,70°+∠BDE =180°よって,∠ BDE =110°・・・1次に, EDCについて2つの内角の和が他の角の外角に等しいので. 円に内接する四角形 - Wikipedia. 円に内接する四角形の例. 円に内接する四角形 (えんにないせつするしかっけい、 英: cyclic quadrilateral )または単に 内接四角形 (ないせつしかっけい、 英: inscribed quadrilateral )とは、4 頂点 が1つの 円周 上にある 四角形 のことである [1] 。 この円のことを 外接円 といい、その上にある4頂点は 共円 であるという。 一般的に、内接四角形は 凸 であると仮定されるが、四角形が自己交差することを許せば凸でない内接四角形も存在する。 以下では凸四角形に限って述べることとする。 すべての 三角形 が外接円を持つのに対して、すべての四角形が外接円を持つとは限らない。. 円に内接する四角形 | 無料で使える中学学習プリント. 数学. 円 に 内 接する 四角形 半径中3数学. 円 に 内 接する 四角形 半径円に内接する四角形には次の性質があります。 1 円に内接する四角形の対角の和は180°. 円 に 内 接する 四角形 半径2 四角形の内角は、その対角の外角に等しい. 円 に 内 接する 四角形 半径この性質を使って角度を求めたり、証明問題を解いたりします。 1 円に内接する四角形の対角の和は180° の証明. 上の図で四角形ABCDが円に内接するとき ∠B=a ∠D=bとすると. 円の中心角は円周角の2倍 の大きさにあたるので. ∠AOC=2b(赤い線) ∠AOC=2a(青い線) つまり 2a+2b=360° 両辺を2で割ると a+b=180°. 円 に 内 接する 四角形 半径よって 円に内接する四角形の対角の和は180° になる。 2 四角形の内角は、その対角の外角に等しい の証明. 上の図で ∠ADCの外角=180−b. 【基本】三角比と円に内接する四角形 | なかけんの数学ノート. 円に内接する四角形 がある。 AB = 4, BC = 5, CD = 4, ∠ B = 60 ∘ とする。 このとき、 と AD の長さを求めなさい。 図をかくと、次のような状況です。 まず、三角形 について余弦定理を使うと. AC 2 = 4 2 + 5 2 − 2 ⋅ 4 ⋅ 5 ⋅ cos 60 ∘ = 16 + 25 − 20 = 21 なので、 AC = 21 となります。 次に、 を出すために、三角形 について考えます。 と先ほど求めた しかないように見えますが、四角形 が円に内接していることから、 ∠ D = 120 ∘ がわかります。 これを利用して余弦定理を使います。 AD = x とすると. 円 に 内 接する 四角形 半径円に外接する四角形とその性質 | 高校数学の美しい物語. 例えば,円に外接する四角形がさらに別の円に内接する場合,円に内接する四角形の性質より θ 1 + θ 2 = 18 0 ∘ theta_1+theta_2=180^{circ} θ 1 + θ 2 = 18 0 ∘ なので S = a b c d S=sqrt{abcd} S = ab c d となります。. 【解説】三角錐に内接する球の半径を求めよう │ 理系のひとりごと. 実はこの考え方は三角錐によらず、あらゆる多面体に対して使うことができます。. これを一般的な公式として表したのが次の式です。. 多面体の内接球の公式. V = 1 3rS V = 1 3 r S. V V :多面体の体積. S S :多面体の表面積. r r :内接球の半径. ただし公式を丸 . PDF 大小2つの円に接する円. a で円p に接し 円q に接する円を作図しよう。 [図6-1] pq を 円p の半径と 円q の半径の比に 外分する点をr 内分する点をs とする。 r とs が大きな働きをします。 [図6-2] a とs を通る直線を引き 図のようにb, c, d をとる。 a で円p で接し d で円q で接する円が . 円 に 内 接する 四角形 半径松 の 司 純 米 大 吟醸
餃子 の 満州 クーポン接弦定理とは何か。角度別に分かるその証明方法|アタリマエ!. 角度別に分かるその証明方法. 「円の接線 AT A T と弦 AB A B が作る角 ∠BAT ∠ B A T は、弦 AB A B に対する円周角 ∠ACB ∠ A C B と等しい」という定理を、 接弦定理 と言います。. 接弦定理は、 ∠BAT ∠ B A T が鋭角・直角・鈍角のどの場合でも成り立ちますが . 円 に 内 接する 四角形 半径【円の接線作図】基本作図から2つの円の共通接線まで解説! | 数スタ. 今回はコンパスを使って円の接線を作図する方法について解説していくよ!. 中学で学習する基本的な作図から. 2つの円に接する超難問の作図まで解説していきます!. この記事では接線のかき方をメインにお伝えしていますが、記事の途中に発展的な . 正三角形の内接円の半径と外接円の半径 - 具体例で学ぶ数学. 円 に 内 接する 四角形 半径最終更新日 2019/05/12. 一辺の長さが a a である正三角形の内接円の半径は、. 円 に 内 接する 四角形 半径r = 3-√ 6 a r = 3 6 a. 外接円の半径は、. R = 3-√ 3 a R = 3 3 a. 円 に 内 接する 四角形 半径ペラダン の 復権
鶴見 の 廃 工場いろいろな方法で計算してみます。. 直角三角形を使う方法. 重心を使う方法. 円に内接、外接する正n角形の面積をイチから求めてみよう! | 数スタ. このように、円の半径からは「三角形の高さが1になる」ということしか読み取れません。 斜めの長さがわからない状態では、面積公式が使えないので困ってしまいます… そこで!次の直角三角形に注目しましょう!. 円と接線に関する3定理(垂直、接線の長さ、接弦定理). 円と接線に関する3定理(垂直、接線の長さ、接弦定理). 2019.06.18. 検索用コード. 円 に 内 接する 四角形 半径円の接線は, 接点を通る半径と垂直をなす. 円の外部の点から引いた2本の接線の長さは等しい. 正負 の 数 の 加減
水垢 セスキ接点を通る弦と接線が作る角は, その角内の弧に対する円周角に等しい (接弦 . 【高校数学Ⅱ】「2つの円が接する条件」 | 映像授業のTry IT (トライイット). 円 に 内 接する 四角形 半径Try IT(トライイット)の2つの円が接する条件の映像授業ページです。Try IT(トライイット)は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る(トライイットする)ことにより「わからない」をなくすことが出来ます。全く新しい形の映像授業で日々の勉強の . 接する円と曲線 | 教えて数学理科. 接する円と曲線の例題です。 数Ⅲの範囲では「接する=重解」を使うよりも、「円の接線と、接点と中心を結ぶ直線が垂直」という円の基本的な性質を使っていきます。 (例題) (xy)平面において、直線 (x= […]接する円と曲線の例題です。 数Ⅲの範囲では「接する=重解」を使うよりも、「円 . 円に内接する三角形の面積の最大値 | 高校数学の美しい物語. つまり,正三角形でないときは,より面積の大きな三角形を構成できるので,面積を最大にするのは正三角形である(注)。. 重要な注:最後の議論では,最大値の存在を仮定しています。. 1.正三角形でないときは改善できる. 2.最大値が存在する. の両方 . 円 に 内 接する 四角形 半径東北学院 円に外接する四角形 四角形と内接円の半径 - YouTube. オンラインプロ家庭教師してます。zoomを利用して直接川端が指導します。 ホームページはこちらhttps://sites.google.com/view . 円に内接する四角形. 円 に 内 接する 四角形 半径大きな区分. [用語] 四角形の4つの頂点が1つの円周上にあるとき,この四角形は 円に内接する といいます.. 円に内接する四角形の 向かい合う内角の和 は180゜に等しい.. 左図の∠Aと∠Cは向かい合う内角です.左図の∠Bと∠Dも向かい合う内角です.. 次の . 内接円の半径の求め方!楽に求める時間の節約術とは?|高校生向け受験応援メディア「受験のミカタ」. 内接円の半径の求め方が誰でも理解できる記事です。これを読めば、内接円に関する事項がすべて理解できるでしょう。扱う内容は、内接円とは何か・内接円の半径を求める公式と証明・練習問題です。充実の内容なので、ぜひご覧ください。. 外接円とは?半径の公式や求め方、性質をわかりやすく解説! | 受験辞典. この記事では、「外接円」についてできるだけわかりやすく解説していきます。 外接円の半径の公式や求め方、外接円の性質についても説明していくので、この記事を通してぜひマスターしてくださいね。 目次外接円とは?三角形の外接 . 円に内接する正多角形 - 高精度計算サイト. 円に内接する正多角形の辺の長さと面積の表を計算できる高精度計算サイトです。カシオ計算機の製品やサービスに関する情報も掲載しています。円の半径や角数を入力するだけで、簡単に正多角形の性質を知ることができます。. 外接円の半径と内接円の半径の関係 | 高校数学の美しい物語. 著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください! レベル: . 外接円の半径と三角形の面積の関係(S=abc/4R) 三角形の内角における和積公式 . 【標準】2つの円が交わる条件 | なかけんの数学ノート. 円 に 内 接する 四角形 半径ここでは、2つの円が交わる条件を求める問題を見てきました。. 2つの異なる共有点を持つ条件を求めるには、内接するとき・外接するときを基準に考えて解きます。. また、内接するとき・外接するときの半径を求めるには、2つの円の中心間の距離と接点と . 図形の性質|2円の位置関係について | 日々是鍛錬 ひびこれたんれん. さいごに、もう一度、頭の中を整理しよう. 今回は、2円の位置関係について学習しましょう。. 均整 院 と は
妊娠 出産 と 健康 指導 案この単元に関する問題は、新課程以前ではよく出題されていました。. それに対して新課程になると、あまり見かけなくなりました。. あくまでも傾向なので . 数学aの円で使う定理・性質の一覧 - マナペディア. 円 に 内 接する 四角形 半径10. ヨーロッパ諸国の海外進出(ヨーロッパ各国のアジア・新大陸植民地など) 受験対策問題 62. 円 に 内 接する 四角形 半径数学Aの円で使う定理・性質の一覧 円周角の定理 弧ABに対する円周角の大きさはつねに一定であり、その角の大きさは、その弧に対する中心角の大きさの半分で . 円 に 内 接する 四角形 半径2つの円に接する円の半径(東京都立大2020理系第2問) - mm参考書. 2つの円に接する円の半径 (東京都立大2020理系第2問) 公開日:2021/05/30. ぐっさんの ハッピー オン ステージ
最終更新日:2021/05/30. 円 A A と円 B B と直線 l l がそれぞれ異なる点で接しているとする。. A A と l l の接点を text {P}_A PA とし, B B と l l の接点を text {P}_B PB とする。. 円 に 内 接する 四角形 半径C_1 C 1 を A A と B B と l . 内接球の半径を求める公式と例題・証明 | 高校数学の美しい物語. 内接球とは,多面体のすべての面に接する球のことです。 内接球の半径の求め方について,例題・公式の証明・補足を述べます。 . よって,2次元バージョン,つまり内接円の半径を求める公式の証明を理解できれば内接球もすぐに理解できます。 . 【基本】2つの円と共通接線 | なかけんの数学ノート. そこで使えるのが、 共通接線 です。. 2つの円のどちらにも接する直線のことです。. 例えば、内接する場合は、次のように、共通接線は1本だけ引くことができます。. 2つの円の接点を通る直線です。. 一方、外接する場合は、同じように2つの円の接点を . 8 - 円2 - 接点・接点・半径で円を描く | AutoCAD 使い方徹底ナビ. [リボン]-[ホーム]タブ-[作成]パネル-[円(中心、半径)]をクリックします。 「円の中心点を指定 または:」と表示されたら作業領域内で右クリックし、ショートカットメニューの中から[接、接、半(t)]を選択します。 「円の第1の接線に対するオブジェクト上の点を指定:」と表示されたら新たに . 円 に 内 接する 四角形 半径なぜ、"円の接線は、接点を通る半径に垂直"になるのか?を説明します|おかわりドリル. 円 に 内 接する 四角形 半径数学で習う円に接する直線は、その接点を通る半径と垂直になります。では、なぜ垂直になるのでしょうか?疑問に思ったときや、お子さんから質問されたときに、ぜひ参考にしてみてください。無料でたのしい学習コンテンツはおかわりドリル。. 接点間の距離に関する有名問題4問(共通接線上の長さなど). 共通外接線の接点間の距離. 問題1. 半径が 3,5 3,5 であり,中心間の距離が 9 9 である2つの円がある。. 接点間の距離 AB AB を求めよ。. 解答. 図のような直角三角形 O_1O_2H O1O2H に三平方の定理を使うと,. AB=O_1H=sqrt {9^2- (5-3)^2}=sqrt {77} AB = O1H = 92 − (5− 3)2 = 77 . 円 に 内 接する 四角形 半径【発展】円に内接する正五角形の作図(デザインあ おとなスペシャル2020で紹介されてたやつ) | なかけんの数学ノート. 大学数学基礎. 数の構成. ここでは、円に内接する正五角形の作図方法について詳しく見ていきます。. 2020年の1月に放送された「デザインあ おとなスペシャル」でも紹介されていた作図方法ですが、ここでは辺の長さを求めるところも考えます。. なお . 2つの円の位置関係と円の半径・中心間の距離 | 高校数学の知識庫. 円 に 内 接する 四角形 半径見出しにもあるとおり、円同士の関係を決めているのは . 2つの円の中心の距離 . と . 2つの円の半径 . です。例えば円同士が全く交点を持たない場合というのは一つ目に . こんなのが考えられます。これは2つの円が 「互いに外部にある」 とよく呼ばれます . 円 に 内 接する 四角形 半径円と正方形で覚えるルールはこの2つ!―「中学受験+塾なし」の勉強法!. この記事では「円と正方形」についてまとめています。 いわゆる「図形」の問題になります。 円と正方形. ルール1! 【円の中の正方形の面積は、その円の半径を1辺とする正方形の面積の2倍】 「円に内接する正方形」の図は算数の問題でよく出てきますが、. 二つの円に接する共通接線 - 高校数学.net. 点と直線の距離の公式を利用. 一つ目の円で接点を(small{ (x_1, y_1) })とおいて公式から導いた接線の方程式がもう一つの円に接することを点と直線の距離の公式を使って求めよう。. 円の中心と直線の距離が円の半径に等しいとき円とその直線は接するから、二つ目の円の中心と半径を求め . 円錐と内接球・その1 | 中学数学の無料オンライン学習サイトchu-su-. 問題下の図のように、底面の半径が (28cm),母線の長さが (100cm) の円錐に球が内接しています。この球の半径を求めなさい。 解説平面における、「三角形と内接円の関係」とほぼ同じです。空間図形においても、着目すべき「平面」で解きます。. 四角形が円に外接するための必要十分条件|思考力を鍛える数学. 円に内接する四角形はメジャーですが,今回はそれよりもマイナーな,円に外接する四角形についてです.どのような三角形も必ず内接円をもちます.つまり,三角形の $3$ 辺と接するような円が存在します.ところが,四角形の場合はそうではありません . 円 に 内 接する 四角形 半径【AutoCAD 初心者】3 つの図形に接する円を作成する方法 - メモだよ!!. 円 に 内 接する 四角形 半径円を作成するドロップダウンの中に、[接点、接点、接点]というものがあります。 これをクリックすると、3 つの図形に接する円を作成できます。 ホーム タブにある[接点、接点、接点]ボタンをクリックします。 ひとつめの図形をクリックします。. 円に関する性質その1(接弦定理) - 高校数学の知識庫. 接弦定理. 円 に 内 接する 四角形 半径接弦定理 は「円に内接する三角形とその円に接する接線があり、かつ三角形の"ある"頂点が接点となっている」場合に考えることができます。. 次のような状態の時ですね。. 三角形が円に「内接」しているのがわかります。. また円に接線が . 【標準】円の接線と作図 | なかけんの数学ノート. 円の中心と接点とを結んだ線分は、接線と垂直となります。. 円 に 内 接する 四角形 半径ということは、点 から、直線 ℓ に垂線をおろせば、交点が接点となります。. 円 に 内 接する 四角形 半径【基本】垂線の作図(直線上にない点を通る)その2 で見た内容などを使えば、垂線を作図することができるので . 解き方を教えてください半径5cmの円に内接する正方形の面積を求めな. - Yahoo!知恵袋. 解き方を教えてください半径5cmの円に内接する正方形の面積を求めなさい。よろしくお願いします。 半径5cmに円に内接する正方形は、その対角線が円の直径になりますので対角線の長さは10cmその面積は10×10÷2=50cm^2. 円に内接する四角形の面積ブラーマグプタの公式(裏技)の証明と円に内接しない四角形の面積ブレートシュナイダーの公式(裏技). 三角形の外接円の半径、内接円の半径と面積の関係 S=1/2r(a+b+c) 三角形の頂角の二等分線の長さ:基本2パターン、裏技公式 x=√(ab-cd) とその証明; 中線定理(パップスの定理)とスチュワートの定理の三角比による証明. 【中学数学】作図・円と接線、接点 | 中学数学の無料オンライン学習サイトchu-su-. 接線の作図例題1円 (o) の周上の点 (a) で、円 (o) に接する接線を作図しなさい。解答まずは完成図をラフスケッチしましょう。接線は、中心と接点を結ぶ半径と垂直になる。これは重要暗記事項ですよ。よって、(oa) を引き、点 (a) を通る、(oa) の垂線 . 空間内の3点を通る円 | 自由気ままにWebノート. 円 に 内 接する 四角形 半径空間内の3点を通る円. TMyuki 代数学, 幾何学, 数学 0 Comments. Tweet. 原点を O ( 0, 0, 0) とする空間内の一直線上に並んでいない3点. P 1 ( x 1, y 2, z 3), P 2 ( x 2, y 2, z 2), P 3 ( x 3, y 3, z 3) を通る円 C の中心 C ( c 1, c 2, c 3) と半径 r ,円弧のパラメータ表示を求める . 長方形に内接する2つの円 | 中学数学の無料オンライン学習サイトchu-su-. 問題下図のように、長方形の (2) つの辺に内接する半径の等しい (2) つの円があり、円どうしも接しています。このとき、円の半径を求めなさい。 解説求める円の半径を (rcm) とします。 円と接線ですから、中心と接点を結びます。基本知識です。. 半径rの円に内接する長方形のうち、面積が最大となるものを求めなさい。 - . - Yahoo!知恵袋. 半径rの円に内接する長方形のうち、面積が最大となるものを求めなさい。 この問題は、どうやって解くか教えてください。お願いします! 長方形の各頂点から対角線を引くと円の中心で交わりますね。その一つの角をθ(0<θ<π)とするともう一つはπ-θ、円の半径をrとします。長方形は対角線 . AUTOCADで点と接する円と半径が決まっている場合、どうすれば接円を. - Yahoo!知恵袋. AUTOCADで点と接する円と半径が決まっている場合、どうすれば接円をかけますか?接点・接点・半径では、今回は、一箇所、点が決まっているため書けませんでした。 点Aと円Bが図のように位置していたとします。青い円が目的の円です。・青円と赤円の中心を結んだ直線は図の黒直線になり . 正多角形の内接円の半径・外接円の半径 | 高校数学の美しい物語. 円 に 内 接する 四角形 半径更新 2023/09/16. 1辺の長さが a a である正多角形の 内接円の半径 と 外接円の半径 を考えます。. 内接円の半径. 正三角形の 内接円の半径 は. 3 6 a ≒ 0.289 a. 円 に 内 接する 四角形 半径dfrac {sqrt {3}} {6}afallingdotseq 0.289a 63. a ≒ 0.289a. 正方形の内接円の半径は. 《円・半円・弧・扇形》の円周・面積の求め方と公式一覧|小学生の算数 | Yattoke! - 小・中学生の学習サイト. 円の面積 円の面積と円周の公式はどっちがどっちだか わからなくなることがありますのでしっかり確実に覚えておくようにしましょう。 円の面積 = 半径 × 半径 × 円周率 弧の面積 まず、円の面積を求めて、そのうちの弧の角度分の面積を知りたいので、.